IceSandwich

排序（一）

描述排序算法原理

算法
字数统计: 2.4k阅读时长: 12 min
2019/01/19 Share

排序的算法有很多种，其中冒泡排序、选择排序、插入排序我喜欢把它们叫隔板排序（这名字我瞎想的别出去乱说啊），因为排序的时候会有明显的分界，一边是排序好的另一边是未排序的，就好像有个板将它们隔开一样。隔板排序的方法都很相似，需要两重循环，一个控制隔板，一个进行比较和交换功能。

 

前言

由于每次排序都需要一个main函数输入一堆数字，不方便重点关注算法本身，于是我写了一个头文件，之后的排序算法就使用这个模板了，并且无特殊说明，统一为从小到大排序。

头文件： SortUtils.hpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <iostream>
#include <sys/time.h>
#define MAXN 1000
int __nums[MAXN], __compare = 0, __swap = 0; //统计比较和交换次数

void Sort(int[], int); //需要实现的函数
void Swap(int, int);
int Compare(int, int);

void Swap(int i, int j) {
    ++__swap;
    int t = __nums[i]; __nums[i] = __nums[j]; __nums[j] = t;
}

int CompareTo(int i, int j) {
    ++__compare;
    return __nums[i]-__nums[j];
}

int main() {
    using namespace std;
    int N = 0; //记录数组长度
    for (int t; cin>>t; ++N) __nums[N] = t; //输入数字，以EOF结束

    cout<<"Source Array: "; //输出原数组
    for (int i = 0; i < N; ++i) cout<<__nums[i]<<' ';

    struct timeval start, stop; //统计排序所用时间
    gettimeofday(&start, NULL);
    Sort(__nums, N); //排序
    gettimeofday(&stop, NULL);


    cout<<"\nSorted Array: "; //输出排序数组
    for (int i = 0; i < N; ++i) cout<<__nums[i]<<' ';
    
    cout<<endl; //之后输出统计结果
    cout<<"| Array Length: "<<N<<endl;
    cout<<"|   Swap times: "<<__swap<<endl;
    cout<<"|Compare times: "<<__compare<<endl;
    cout<<"| Run time(μs): "<<(stop.tv_usec-start.tv_usec)<<" μs\n";
    cout<<"| Run time(ms): "<<(stop.tv_usec-start.tv_usec)/1000.0<<" ms\n";
    return 0;
}

样例文本: SampleInput.txt

1
33 12 89 56 77

编译和运行方式：遵从GCC标准

1
g++ SortFile.cpp -o sort.out && ./sort.out < SampleInput.txt

其中SortFile.cpp对应下面的代码文件。

 

冒泡排序

1
2
3
4
5
6
7
8
#include "SortUtils.hpp"

void Sort(int a[], int n) {
    for (int i = n-1; i >= 0; --i) //控制隔板位置
        for (int j = 0; j < i; ++j) //进行比较和交换操作
            if (CompareTo(j, j+1)>0)
                Swap(j, j+1);
}

这个代码的隔板是从右边往左移动的，将最大的往后走，过程如下：

如果你想变量i从0开始，也可以这样：

1
2
3
4
for (int i = 0; i < n; ++i) //控制隔板位置
	for (int j = 0; j < n-i-1; ++j) //进行比较和交换操作
		if (CompareTo(j, j+1)>0)
        	Swap(j, j+1);

或者你想隔板从0开始也可以：

1
2
3
4
for (int i = 0; i < n; ++i) //控制隔板位置
	for (int j = n-1; j > i; --j) //进行比较和交换操作
    	if (CompareTo(j, j-1)<0)
        	Swap(j, j-1);

无论怎样，都是同样的算法，同样的结果：

1
2
3
4
5
6
7
Source Array: 33 12 89 56 77
Sorted Array: 12 33 56 77 89
| Array Length: 5
|   Swap times: 3
|Compare times: 10
| Run time(μs): 3 μs
| Run time(ms): 0.003 ms

 

选择排序

1
2
3
4
5
6
7
8
9
10
11
#include "SortUtils.hpp"

void Sort(int a[], int n) {
    for (int i = n-1; i >= 0; --i) {
        int max = i;
        for (int j = 0; j < i; ++j)
            if (CompareTo(j, max)>0)
                max = j;
        Swap(max, i);
    }
}

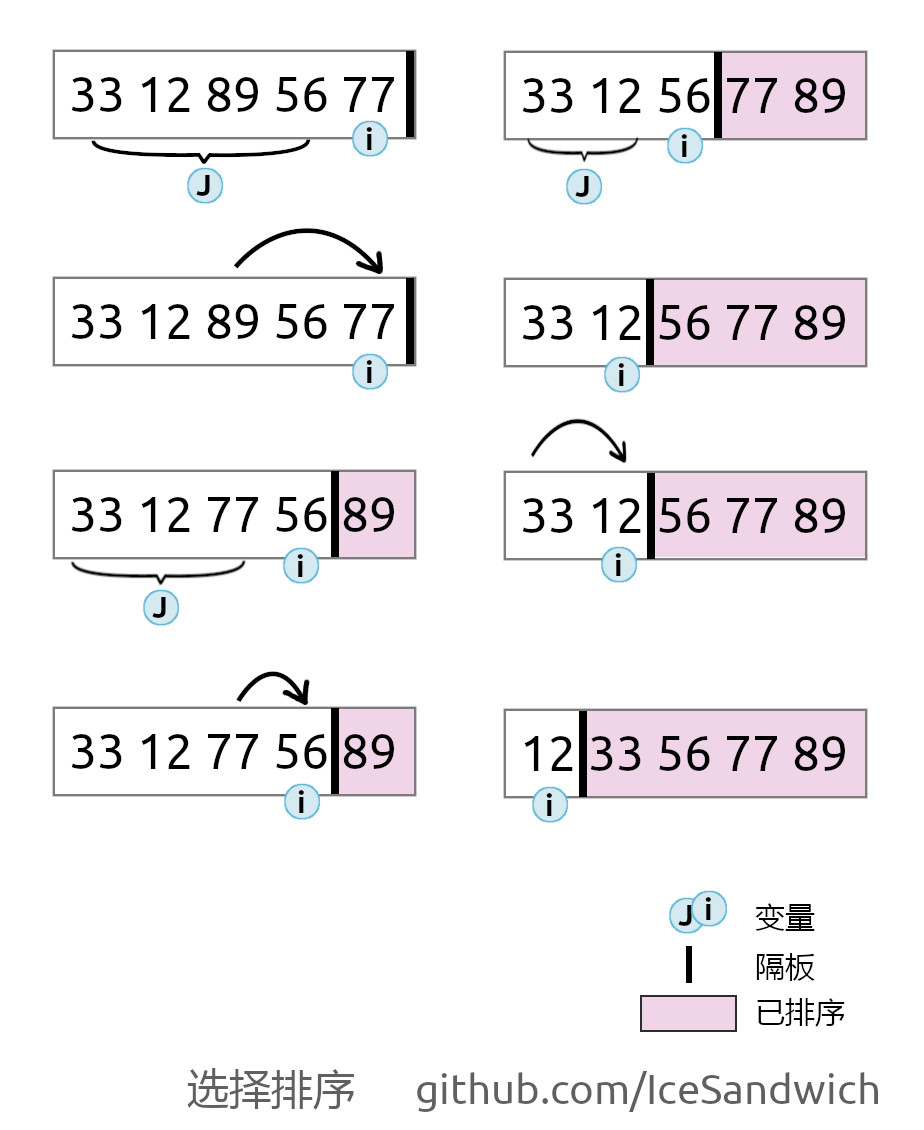
过程如下：

选择排序个人喜欢叫他选择最大/最小排序，从未排序的数字选择最大/最小的数字与隔板后第一个数交换。

当然你可以像冒泡排序一样，随意更改隔板顺序：

1
2
3
4
5
6
7
for (int i = 0; i < n-1; ++i) {
    int min = i;
    for (int j = i+1; j < n; ++j)
        if (CompareTo(j, min)<0)
            min = j;
    Swap(min, i);
}

最后结果还是一样的：

1
2
3
4
5
6
7
Source Array: 33 12 89 56 77
Sorted Array: 12 33 56 77 89
| Array Length: 5
|   Swap times: 5
|Compare times: 10
| Run time(μs): 3 μs
| Run time(ms): 0.003 ms

不同的是Swap次数，更改隔板顺序后Swap times变成4了，不知道什么原因。。。

 

插入排序

插入排序更符合生活想法，毕竟我们排序都是这样的。

1
2
3
4
5
6
7
#include "SortUtils.hpp"

void Sort(int a[], int n) {
    for (int i = n-1; i >= 0; --i)
        for (int j = i-1; j < n-1 && CompareTo(j, j+1)>0; ++j)
            Swap(j, j+1);
}

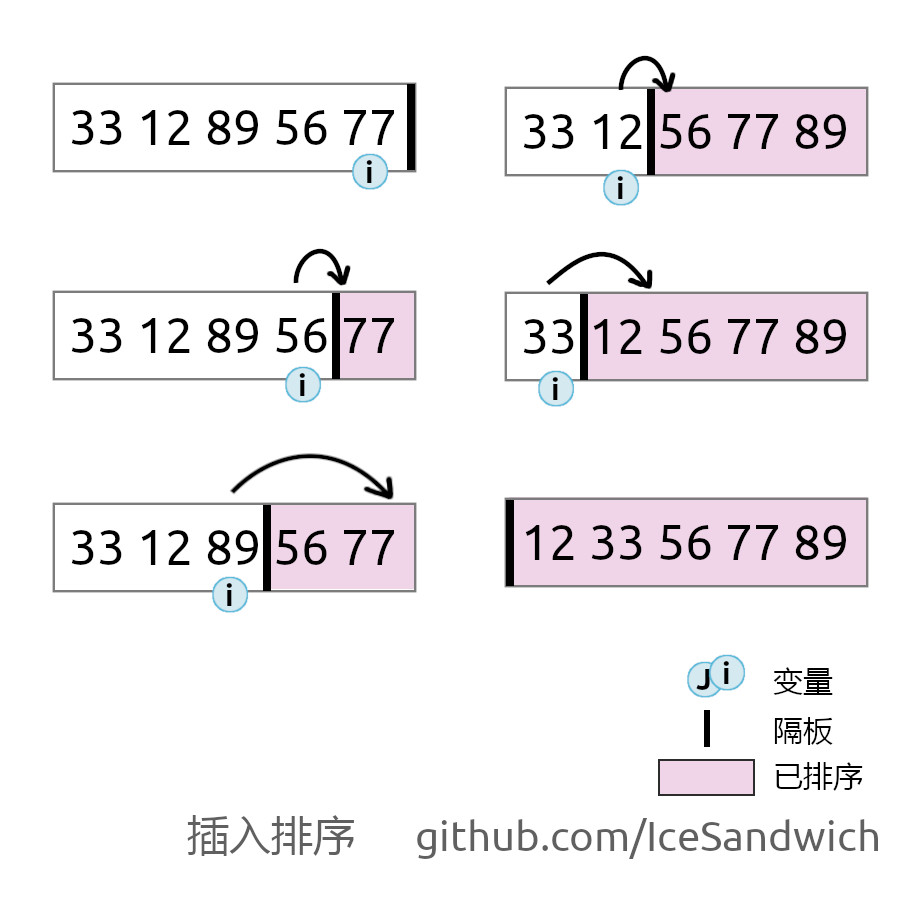
过程如下：

结果如下：

1
2
3
4
5
6
7
Source Array: 33 12 89 56 77
Sorted Array: 12 33 56 77 89
| Array Length: 5
|   Swap times: 3
|Compare times: 7
| Run time(μs): 3 μs
| Run time(ms): 0.003 ms

 

希尔排序

希尔排序其实是利用插入排序的优点提高排序的效率的，从上面的代码可以看到，冒泡排序、选择排序、插入排序的时间复杂度是O(N2)，这个复杂度还是比较大的，希尔排序的复杂度比插入排序的低，但是具体是多少，目前是没办法研究的，因为希尔排序需要选择一个基数，而这个基数将决定了复杂度在哪个范围。当gn+1=3gn+1时，算法的复杂度维持在O(N1.25)，比前面的排序方法都要好。

那。。。插入排序的优点是什么？当输入的数组比较有序的时候，插入排序更快。希尔排序充分利用这个思想，把相隔几个的数字排序，然后这几个数字就较有序了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include "SortUtils.hpp"

void InsertSort(int a[], int s, int e, int step) {
    //对 s s+step s+2*step ...  s+n*step 进行插入排序，保证s+n*step < e
    int n = (e-1-s)/step, last = s+n*step;
    for (int b = last; b >= s+step; b -= step) //b为隔板位置，从右边往左边移动
        for (int i = b - step; i <= last-step && CompareTo(i, i+step)>0; i += step)
            Swap(i, i+step);
}

void Sort(int a[], int n) {
    //采用G(n+1)=3G(n)+1的增量
    for (int g = n/3+1; g > 1; g=g/3+1)
        for (int i = 0; i < g; ++i)
            InsertSort(a, i, n, g);
    InsertSort(a, 0, n, 1);
}

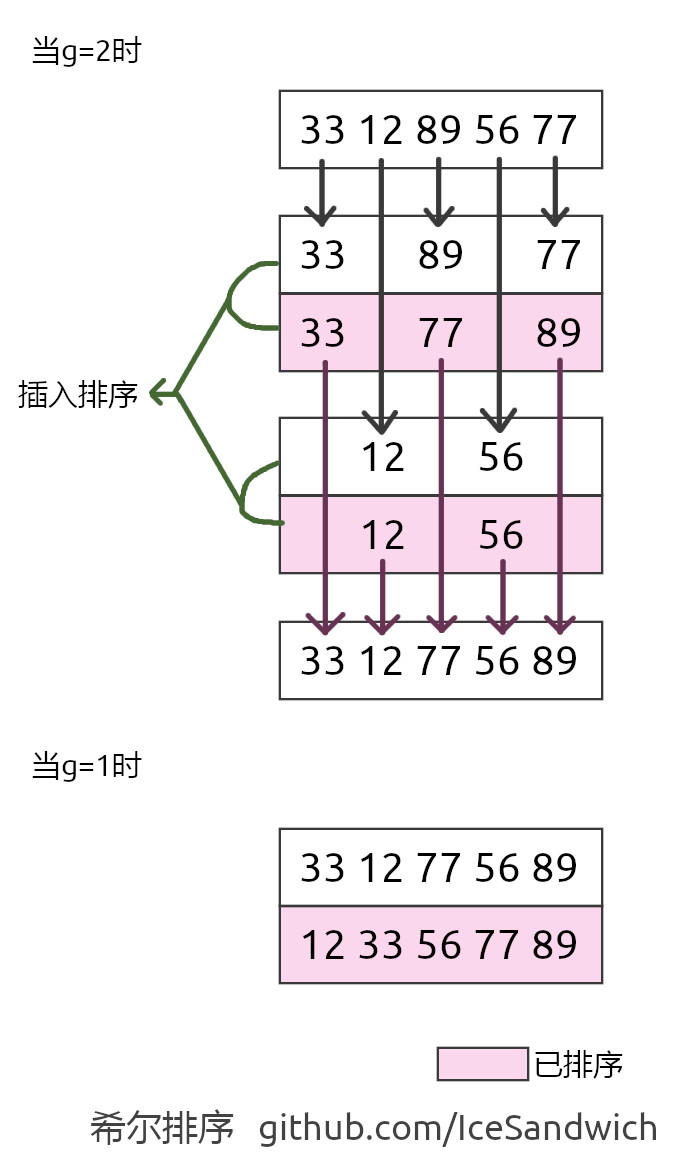
示意图如下：g的两个取值由来：(g=n/3+1=5/3+1=2) (g=2/3+1=1)

如果用上面的样例测试的话，几乎看不出效果：

1
2
3
4
5
6
7
Source Array: 33 12 89 56 77
Sorted Array: 12 33 56 77 89
| Array Length: 5
|   Swap times: 3
|Compare times: 9
| Run time(μs): 4 μs
| Run time(ms): 0.004 ms

当数据比较大的时候才看出效果，为了向大家解释希尔排序，但我又不想做图…干脆从程序输出运算过程：

样例：

1
4 9 2 1 0 4 3 9 6 5 7 8 1 0 2

运算过程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
g: 6
 Source Array: 4 9 2 1 0 4 3 9 6 5 7 8 1 0 2
    Sub array: 4           3           1
SortSub array: 1           3           4
    Sub array:   9           9           0
SortSub array:   0           9           9
    Sub array:     2           6           2
SortSub array:     2           2           6
    Sub array:       1           5
SortSub array:       1           5
    Sub array:         0           7
SortSub array:         0           7
    Sub array:           4           8
SortSub array:           4           8
 
g: 3
 Sorted Array: 1 0 2 1 0 4 3 9 2 5 7 8 4 9 6
    Sub array: 1     1     3     5     4
SortSub array: 1     1     3     4     5
    Sub array:   0     0     9     7     9
SortSub array:   0     0     7     9     9
    Sub array:     2     4     2     8     6
SortSub array:     2     2     4     6     8

g: 2
 Sorted Array: 1 0 2 1 0 2 3 7 4 4 9 6 5 9 8
    Sub array: 1   2   0   3   4   9   5   8
SortSub array: 0   1   2   3   4   5   8   9
    Sub array:   0   1   2   7   4   6   9
SortSub array:   0   1   2   4   6   7   9
 
g: 1
 Sorted Array: 0 0 1 1 2 2 3 4 4 6 5 7 8 9 9
    Sub array: 0 0 1 1 2 2 3 4 4 6 5 7 8 9 9
SortSub array: 0 0 1 1 2 2 3 4 4 5 6 7 8 9 9

 

性能比较

如同上面所说，需要大数据才能体现代码的优越性，因此，我用python生成1000个随机数，部分样例如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
8397 3334 5296 3781 4722 2087 4012 7237 2765 7861 7848 3945 8761 3086 1994 7187 8852 1504
2799 8536 8966 955 1285 8034 6463 6329 633 5248 5156 3716 8672 9039 9471 890 4220 8580 
4451 6794 4285 5128 2267 6999 3867 8824 9758 8531 3348 3534 3360 3803 8251 5326 3646 8704 
5751 5373 226 778 503 4875 6427 9778 6505 2639 8839 6199 5223 5037 7279 4264 4063 7809 
6760 9631 4122 8123 2026 7166 6718 3880 4506 1362 2655 1739 991 9875 9801 7271 7631 2619 
3461 129 6043 3650 2195 5630 5871 8346 7323 9328 6237 1447 7338 3441 1182 9977 9690 3186 
5190 4578 2133 1359 1059 6117 5415 8654 7527 8011 9578 7443 3104 1742 1382 1848 1530 7152 
3258 9563 9204 8916 3768 6892 4037 691 7605 7201 1453 3957 5046 7817 7699 5035 80 4804 811 
3595 1865 2138 5192 5159 7513 6395 7621 8389 7446 1646 6977 6963 3229 983 1118 1393 6026 
9220 2486 8148 2863 8294 7800 7766 5746 1244 3332 6201 7096 6254 8423 237 2314 6901 5693 
2400 7433 4649 8108 633 6955 5468 6433 7165 29 412 2783 7913 8455 95 6269 3573 9963 1113 
6389 3095 8721 365 5490 7430 9160 5220 1291 603 7197 6749 6485 1892 3986 1631 5792 6809 
7520 6136 949 5527 3217 ......

同时，1000个数我不可能输出吧，所以对SortUtils.hpp进行了些改动，首先取消输出原数组和排序后的数组，但是不输出排序后的数组我怎么知道它是有序的呢？于是写一个函数：

1
2
3
4
5
6
7
bool Check(int n) {
    for (int i = 0; i < n-2; ++i) {
        if (__nums[i] > __nums[i+1])
            return false;
    }
    return true;
}

在main里执行完Sort函数后调用：

1
cout<<"| Check Sorted: "<<(Check(N)?"yes":"no");

好了，所有都准备就绪了，进行测试，然后测试结果如下：

首先是冒泡排序：

1
2
3
4
5
6
| Check Sorted: yes
| Array Length: 1000
|   Swap times: 248965
|Compare times: 499500
| Run time(μs): 4912 μs
| Run time(ms): 4.912 ms

接着是选择排序：

1
2
3
4
5
6
| Check Sorted: yes
| Array Length: 1000
|   Swap times: 999
|Compare times: 499500
| Run time(μs): 6780 μs
| Run time(ms): 6.78 ms

然后是插入排序：

1
2
3
4
5
6
| Check Sorted: yes
| Array Length: 1000
|   Swap times: 248965
|Compare times: 249959
| Run time(μs): 2850 μs
| Run time(ms): 2.85 ms

之后是希尔排序：

1
2
3
4
5
6
| Check Sorted: yes
| Array Length: 1000
|   Swap times: 7727
|Compare times: 13779
| Run time(μs): 263 μs
| Run time(ms): 0.263 ms

这个明显了，只有希尔排序的执行时间<1ms，说明了希尔排序还是很高效的。

当然我只是测试了一次，没有取平均值，如果你们很是怀疑的话，赶紧去试试吧～

下篇     算法：排序（二）

原文作者：IceSandwich

原文链接：https://icesandwich.github.io/2019/01/19/%E6%8E%92%E5%BA%8F%E4%B8%80/

发表日期：January 19th 2019, 12:00:00 am

更新日期：December 11th 2019, 9:44:42 pm

版权声明：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. 前言
  2. 2. 冒泡排序
  3. 3. 选择排序
  4. 4. 插入排序
  5. 5. 希尔排序
  6. 6. 性能比较
Total : 21
2021
2020
2019
c docker 算法 GTK 三维重建 KinectFusion 稠密重建 MSSQL html gtk opencv cuda BundleFusion 油猴脚本 js esp8266 arduino python torch Premiere FFmpeg 渗透
算法原理 docker GTK 三维重建 gtk BundleFusion 算法 脚本 硬件 研究 FFMPEG 渗透